이전 기사에서는 최대 증거금과 kkt 조건이 어떻게 계산되는지 살펴보았습니다.
이 기사에서는 결정 경계를 찾는 방법을 살펴보겠습니다.
최적화 이론의 이중성(이중성)이란 최적화 문제는 원래 문제입니다(원래 문제)그리고 이중 문제(이중 문제)원칙은 두 가지 관점에서 볼 수 있다는 것입니다.
SVM의 목적함수와 한계는 다음과 같다.

그리고 SVM 방정식을 라그랑주 승수 방정식으로 대체하면 다음이 제공됩니다.
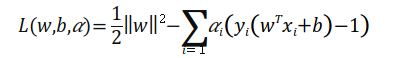
라그랑지안 소수는 위 식으로부터 구할 수 있으며, KKT 조건 #1을 적용하여 w와 b를 편미분하여 구할 수 있다.
라그랑주 소수 방정식은 다음과 같습니다.

앞의 max-expression은 다음 dual-expression의 일부이고 primal을 사용하는 이유는 다음 dual-expression a에 대한 표현식으로 만들기 위함입니다.
w와 b의 편도함수는 다음과 같습니다.
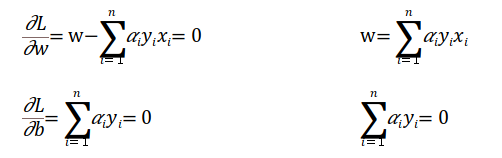
위의 식을 SVM Lagrange multiplier의 식에 대입하면,
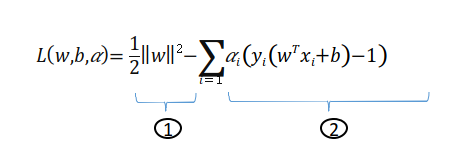
이는 방정식 1과 2를 사용하여 설명할 수 있습니다.
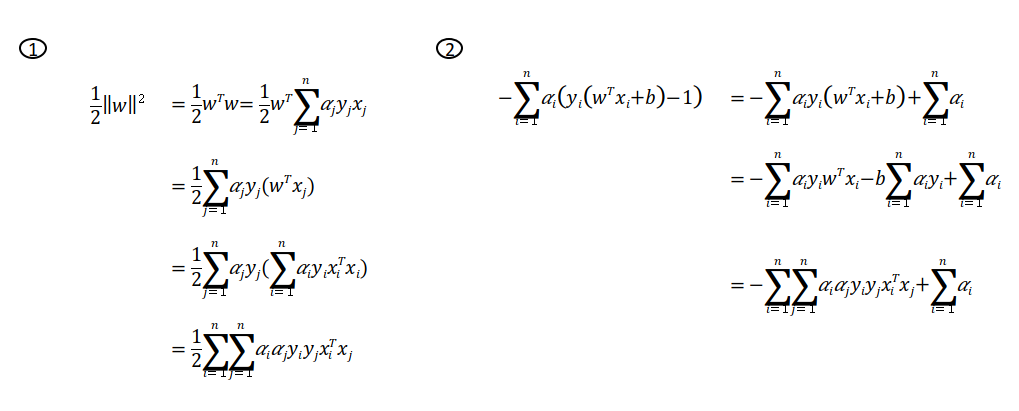
1과 2를 합치면 다음과 같습니다.

위의 방정식을 다시 보면 a에 대한 방정식으로 생성되었으며 위에서 언급한 이중 문제를 해결하기 위한 것입니다.
그러면 위의 방정식은 이중 문제로 변환될 수 있습니다.
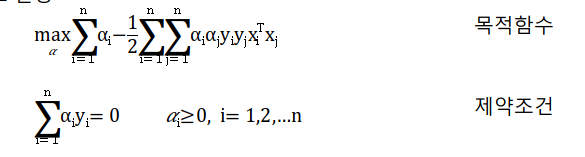
마지막으로 a의 식을 구하면 w와 b의 값을 구할 수 있고, 모든 변수(x, w, b)를 구하면 결정한계의 값을 구할 수 있다.
Decision Boundary는 support vector를 고려하므로 다음 조건을 만족해야 합니다.
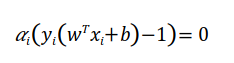
위의 표현은 두 부분으로 나눌 수 있습니다.
1. a>0인 경우

2.a=0

즉, 숫자 1에 대한 식을 만족하며, 숫자 1의 경우 w의 값을 표현하는 식은 다음과 같다.
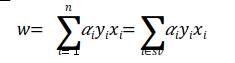
w의 값을 미리 구했다면 모든 점(x)에 대해 구했지만 x는 서포트 벡터의 값에만 영향을 받기 때문에 결정 경계를 구할 수 있고 b의 값은 다음을 이용하여 구할 수 있다. 벡터를 지원합니다.
결정경계식에서 서포트 벡터에 x를 대입하면 w와 y의 값(-1 또는 1)을 알면 b의 값을 알 수 있다.
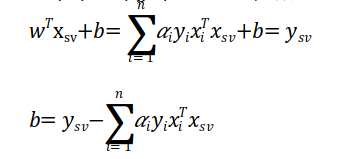
새로운 데이터가 들어옴에 따라 w와 b의 값을 계산하면 새로운 데이터에 대한 분류가 가능하다.
아래 그림과 같이 판정한계 이하이면 -영역(클래스 1)으로, 그 이상이면 +영역(클래스 2)으로 분류할 수 있다.
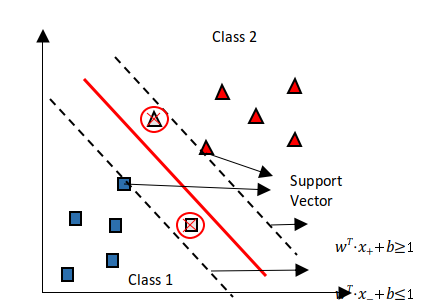
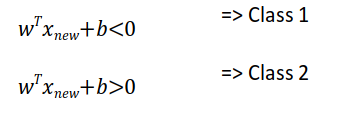
참조